THE GEOMETRIC DISTRIBUTION OF QUEUE LENGTH
UNDER A PREEMPTIVE-RESUME
LAST-COME-FIRST-SERVED
DISCIPLINE
APPROVED:
_________________________________
_________________________________
Copyright
by
Robert
Graham Landrum
1993
DEDICATION
This report is dedicated to my
parents and the memory of Robert Todd Lapsley Liston and of Charles Adair
Bledsoe. These have been the architects of my education.
THE GEOMETRIC DISTRIBUTION OF QUEUE LENGTH
UNDER A PREEMPTIVE-RESUME
LAST-COME-FIRST-SERVED
DISCIPLINE
by
ROBERT GRAHAM LANDRUM, B.S.
REPORT
Presented to the Faculty of the Graduate
School of
The University of Texas at Austin
in Partial Fulfillment
of the Requirements
for the Degree of
MASTER OF ARTS
THE UNIVERSITY OF TEXAS AT AUSTIN
MAY 1993
ACKNOWLEDGEMENTS
The author would like to
acknowledge the direction of Dr. David Fonken in the preparation of this report
and the generousity of Dr. Klaus Bichteler in giving his time to this project.
Dr. Georgia-Ann Klutke's contribution in reading this work is also appreciated.
–
April 19, 1993
Table
of Contents
Chapter
One: Introduction and Explanation of
Notation..................................... 1
Chapter
Two: The Queue Length in G/M/m Systems.......................................... 5
Chapter
Three: M/G/1 (LCFS/I) Systems.......................................................... 12
Chapter
Four: G/G/1 (LCFS/I) Systems............................................................ 20
Chapter
Five: Conclusion.................................................................................. 29
Bibliography...................................................................................................... 31
Chapter
One: Introduction and Explanation of
Notation
A classic example of a queue is a group of patrons lined up
to purchase concert tickets. The two parts of a queueing system consist of a
serving facility (e.g. the ticket booth) and a queueing facility (e.g. the line
of concert goers). In general the queueing facility may consist of a number of
queues as in a supermarket's checkout lines; likewise the serving facility may
have a number of servers. In this report models with one queue and mostly one
server will be considered.
This kind of arrangement is often encountered; however there
are other schemes that approximate other situations and have the advantage of
easier calculation of relevant quantities. Once these calculations have been
made, they may be transferred to a "normal" queue through a
mathematical transformation. The difference in the models is in the queue
discipline, which will be discussed presently.
The notation set out here is based on that of Leonard Kleinrock.
The nth customer, designated by Cn
where n 0, enters the system at tn
. For calculation purposes t0
= 0. The waiting time wn
is the time spent by Cn
in the queue while xn
is the associated service time; furthermore the total system time for Cn is calculated as sn =
wn + xn. The difference tn = tn - tn-1 is the interarrival time between Cn-1
and Cn. For most purposes the tn's and the xn's
are considered to be independent. Now we may define
qn = the
number of customers in the system just after Cn departs.
q'n = the number of customers in the system just
before Cn arrives.
For each n the random variables tn and xn
are the associated with the distribution functions An(t) and Bn(x)
, and these values are the basis for the probabilistic nature of the setup. The
related probability density functions (pdf's) are an(t) and bn(x)
respectively.
If a sequence of random variables converges (in probability)
as n , then the corresponding
limiting variable is denoted with a tilde: 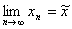 . Limiting distribution functions and their pdf's are written
without a subscript e. g. A(t) and a(t).
. Limiting distribution functions and their pdf's are written
without a subscript e. g. A(t) and a(t).
The following variables may now be defined for the number of
customers in the system:
pk = 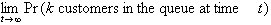
dk = Pr(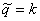 )
)
rk = Pr(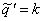 )
)
For 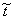 and
and 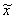 set
set 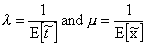 . Define the utilization factor
. Define the utilization factor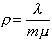 where m is the
number of servers. Since it is the ratio of the average arrival rate to the
average service rate for the system, 0 r 1 in order for an equilibrium state to occur;
otherwise the servers will not be able to handle incoming customers fast
enough.
where m is the
number of servers. Since it is the ratio of the average arrival rate to the
average service rate for the system, 0 r 1 in order for an equilibrium state to occur;
otherwise the servers will not be able to handle incoming customers fast
enough.
The Laplace transform of the variable's pdf will be
represented as
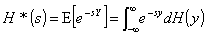 (1.1)
(1.1)
where H(y) = Pr(Y y) is a distribution function.
Similarly the z-transform – also called the generating function – for a
discrete random variable is

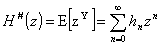 . (1.2)
. (1.2)
Here hn
= Pr(Y = n).
In order to be classified succinctly, queues are designated
with the form A/B/m where A and B stand for the distributions of the
interarrival and service times respectively and m is the number of servers in
the service facility. The distributions are denoted as follows:
G: General
M: (for Markov process)
Exponential
Er:
r-stage Erlangian
HR: R-stage hyperexponential
D: Deterministic
A M/HR/2 queue, for example, has exponentially
distributed interarrival times, services with an R-stage hyperexponential distribution, and employs two servers.
How a customer progresses through the system is described by
the queue discipline. The most common process is the first-come-first-served
(FCFS) discipline where the next customer to be served is the one that has been
in the queue the longest. This is like the concert goers buying tickets. An
alternate scheme is called the last-come-first-served (LCFS) discipline. Here
the next customer for service is the
latest. (This is really a stack but
will be called a queue.)
In this report the last-come-first-served queue discipline
with preemptive resume will be explored usually for queues with one server. Its
designation will be LCFS/I where the "I" stands for
"interrupt." Upon the arrival of a customer into such a system, the
customer in service leaves the server immediately
and enters the queue; the new customer takes up the position with the server.
If the customer with the server completes his service, he leaves the system,
and the last customer to have entered the queue returns to the server. This
will be the customer who was in service when the now departing one arrived.
This report proceeds with a discussion of the intrinsic
geometric nature of G/M/m queues. M/G/1 (LCFS/I) models are then explored
through an intuitive interpretation of
Beneš's inversion of the Polleczek-Khinchin Transform Equation. The last
topic is G/G/1 (LCFS/I) systems with an expansion of the techniques used for
the M/G/1 arrangement.
Chapter
Two: The Queue Length in G/M/m Systems
In this chapter we will discuss the geometric distribution
of queue length under an arbitrary queueing discipline, but the service time
will be assumed to be exponentially distributed.
The mathematical basis for this analysis is the semi-Markov
chain. Let Xn be a random
variable that is paired with a time Tn
where Ti < Tj for i < j. The sequence {Xn,Tn}
is then a semi-Markov chain
if
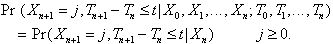 (2.1)
(2.1)
Setting t to leaves
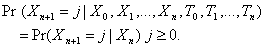 (2.2)
(2.2)
To be as general as possible, it will be assumed that there
are m servers. The development follows that of Kleinrock.
The random variables of the sequence q'n}
form a semi-Markov chain, and the relationship between successive pairs is
easily established:
q'n+1 = q'n
+ 1 - v'n+1 (n 0). (2.3)
Here v'n+1
is the number of customers who finish being served and leave between the
arrivals of Cn and Cn+1
. The transition probabilities are designated
pij
= Pr(q'n+1
= j | q'n = i) (2.4)
or equivalently
pij = Pr(i + 1 - j customers leave during tn+1 | q'n = i). (2.5)
With the v'n's
being nonnegative, it follows immediately that
pij
= 0 for j > i
+ 1. (2.6)
We will concentrate on the situation where i m. Since the service time is exponentially distributed,
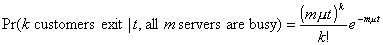 . (2.7)
. (2.7)
Now pij
may be calculated for m j i + 1:
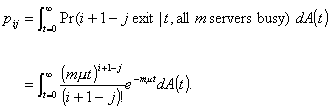 (2.8)
(2.8)
In this last equation the dependence on i and j is in the form i + 1 -
j. Define n = i + 1 - j,
and set
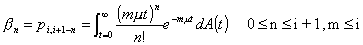 . (2.9)
. (2.9)
bn is the probability that n customers
finish service in an interarrival time given that all m servers are occupied. Let Ek
be the event that there are k
customers in the system, and define
ci(j) = the number of times that the state Ej is reached between successive
visits to Ei.
sk = E( ck(k + 1) ) (k m – 1)
g = Pr( ck+ 1 (j)
= 0, j k) (k m – 1)
= Pr( ck+ 1 (k)
= 0)
Nk(t) = the number of times in (0, t) that an arriving customer finds the
system in state Ek when the system
starts at t = 0 with 0 customers.
Note that g is the same regardless of the value of k. In order to see this, suppose that a
sequence of transitions between states results in ck + 1(k) = 0 where k m – 1. Every such sequence can be matched one-to-one with a
parallel sequence having the same relative transitions but starting with k + 2 customers in the initial
system; furthermore this parallel sequence satisfies ck + 2(k + 1) = 0 and has the same
probability as the first. It is apparent that
Pr(
ck+
1 (k) = 0) = Pr( ck+
2(k + 1) = 0) k
m – 1. (2.10)
The variable sk may be thought of as the ratio of
the times that the system is in state Ek + 1 to the times it is in state Ek. It follows that
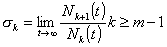 . (2.11)
. (2.11)
If a(t) is the number of customers that have entered
the system in (0, t), then
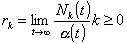 ; (2.12)
; (2.12)
consequently
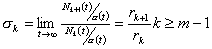 . (2.13)
. (2.13)
From Equation 2.1 it is apparent that if a system goes from
a state Ek to Ek' (k < k'), it can only do so by rising
through successive states; thus if a system in state Ek loses customers before a new customer can arrive, it
must pass through Ek
before reaching Ek + 1. In such a case ck(k + 1) = 0.
This indicates that
Pr(ck(k
+ 1) > 0) = b0. (2.14)
We may now calculate
Pr(ck(k
+ 1) = n) = Pr(ck(k
+ 1) > 0) [Pr(ck + 1(k)
= 0)]n – 1 Pr(ck + 1(k) >
0)
= b0gn –
1(1 – g), (2.15)
and

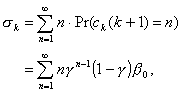 (2.16)
(2.16)
which reduces to
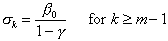 . (2.17)
. (2.17)
Since the right side of this equation does not depend on k, we
may drop the subscript: 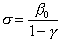 for k m – 1. (2.18)
for k m – 1. (2.18)
From Equation 2.10
rk+
1 = srk
k m – 1 (2.19)
or
rk +
1 = Ksk k m – 1. (2.20)
Here is the geometric relation, but now we need to find K and s. With rk being an equilibrium probability,
the vector r = (r0, r1,
r2,
r3,
. . .) is a solution of the equation r = rP where P = (pij).
Explicitly, when all servers are known to be busy,
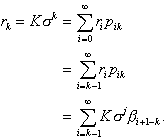 (2.21)
(2.21)
Solving for s, we get
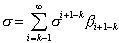 , (2.22)
, (2.22)
which is equivalent to
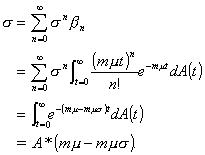 (2.23)
(2.23)
By solving the last equation for a value in (0, 1), s
may be determined. K then follows from the fact that 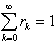 .
.
Theorem: The length of the queue proper given that an
arriving customer finds all servers
busy is geometrically distributed.
Proof. Let Q be the event that an incoming customer
must enter the queue; then
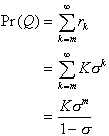 (2.24)
(2.24)
and
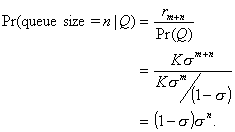 (2.25)
(2.25)
This is the desired result.
Theorem: The number of customers in a G/M/1 system is
geometrically distributed.
Proof:

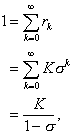 (2.26)
(2.26)
which may be solved to yield
K = 1 – s. (2.27)
The intended result rk = (1 – s)sk easily follows.
The geometric nature of these systems comes from the
circumstance of b0 , g, and thus sk being independent
of k. As was shown earlier, g
was developed without appealing to the underlying probability distributions. On
the other hand, the independence of b0 from k
was evidenced in Equation 2.8 which was derived from the Poisson distribution
of departing customers: the exponential
service times are central to this argument although there is no need for a
special queueing discipline.
Chapter
Three: M/G/1 (LCFS/I) Systems
Although the material in this chapter is less general than
that in the next chapter, it provides an insight into what is actually
occurring with the LCFS/I discipline.
The value of the exponential distribution is that it is
memoryless – that is Pr(t > s+t |t > s) = Pr(t > t).
In the G/M/m case this meant that only the time between arrivals was needed to
calculate the number of departures for that period: the time between the last
departure and first arrival could be "forgotten." For M/G/1 systems
the situation is reversed: since the arrivals are exponentially distributed,
the semi-Markov chain is established on the sequence {qn} of departure times.
3.1. Beneš's Inversion of the Pollaczek-Khinchin Formula for Waiting Time
For this section we need three distribution functions:
Q(t) = Pr(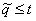 )
)
S(t)
= Pr(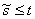 )
)
W(t)
= Pr(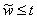 )
)
Q#(z) can be obtained from the
Pollaczek-Khinchin Transform Equation:
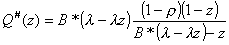 . (3.1)
. (3.1)
Another form of this generating function may be calculated
using the FCFS discipline. In this case all the qn customers in the system when Cn leaves arrive during Cn's system time. Since interarrival times are
exponentially distributed, qn
has a Poisson distribution:
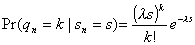 . (3.2)
. (3.2)
Integrating with respect to s and taking the limit as 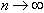 , we get
, we get
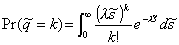 . (3.3)
. (3.3)
Now we calculate
 (3.4)
(3.4)
Setting s = l - lz
and combining Equations 3.1 and 3.4, we get
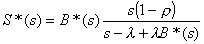 . (3.5)
. (3.5)
The equation 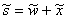 leads to
leads to
S*(s)
= W*(s)B*(s), (3.6)
which may be used to get
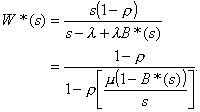 (3.7)
(3.7)
The residual life distribution for the service time is
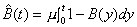 , (3.8)
, (3.8)
and
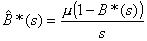 ; (3.9)
; (3.9)
thus
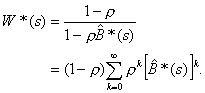 (3.10)
(3.10)
If 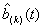 is the k-fold convolution of
is the k-fold convolution of 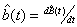 , set
, set

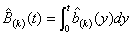 ; (3.11)
; (3.11)
then
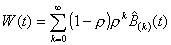 . (3.12)
. (3.12)
3.2. An Attempt to Explain the Formula Directly with a FCFS Discipline
From the results in Chapter Two one may calculate that rk = (1 – r)rk for M/M/1 queues; also since 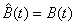 in this case,
in this case, 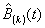 is the probability
that the sum of k service times is
less than t. This suggests that the
following interpretation of Equation 3.12 is plausible:
is the probability
that the sum of k service times is
less than t. This suggests that the
following interpretation of Equation 3.12 is plausible:
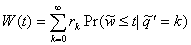 . (3.13)
. (3.13)
Now consider a M/D/1
(FCFS) setup where 
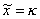 , a constant. In this case
, a constant. In this case
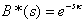 . (3.14)
. (3.14)
From the Pollaczek-Khinchin Transform Equation,
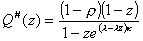 . (3.15)
. (3.15)
Expanding this in a Taylor series, one obtains the dk's as the respective coefficients of
the zk 's. Since 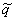 changes by integer
increments, rk = dk and the following table may be
constructed:
changes by integer
increments, rk = dk and the following table may be
constructed:
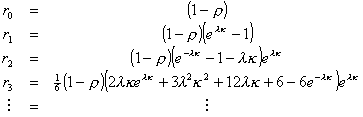 (3.16)
(3.16)
Clearly this is not the geometric distribution intimated in
Equation 3.12; furthermore 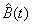 and B(t)
do not generally coincide. Equation 3.12 was useful for calculating purposes
but did not seem to have an intuitive explanation.
and B(t)
do not generally coincide. Equation 3.12 was useful for calculating purposes
but did not seem to have an intuitive explanation.
3.3. Cooper and Niu's Explanation using LCFS/I
Equation 3.13, with a new interpretation for 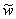 , was shown to be the correct explanation by Robert Cooper
and Shun-Chen Niu in their 1986 article.
The core of their calculations is in the following theorem.
, was shown to be the correct explanation by Robert Cooper
and Shun-Chen Niu in their 1986 article.
The core of their calculations is in the following theorem.
Theorem: The number of customers in a M/G/1 (LCFS/I)
queue is geometrically distributed with rk = (1 – r)rk.
Proof. Define
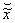 = the residual time for the service after
being interrupted. It has distribution function
= the residual time for the service after
being interrupted. It has distribution function 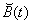 .
.
A queueing system can only reach a state Ek directly either by beginning in Ek –
1 and having a customer arrive or by being in Ek + 1
and losing a customer. In the latter case when a last-come-first-served
arrangement is used, the service time of
the customer then entering service is actually a continuation of the
service period interrupted by the now departing customer: the new service
interval is a residual one. We may now determine that
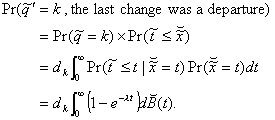 (3.17)
(3.17)
Note that dk
is used as opposed to dk+1 because this random variable refers to
the number of customers after the
departure from the k+1 state. A
similar calculation yields
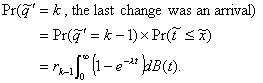 (3.18)
(3.18)
It now follows that
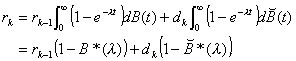 (3.19)
(3.19)
Since a departing customer leaves the system in the same exact
condition as when he arrived, dk
= rk; thus
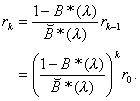 (3.20)
(3.20)
Knowing that r0 = 1 –r and using the normalization condition,
we find that

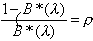 (3.21)
(3.21)
and
rk = (1 – r)rk. (3.22)
Equation 3.21 may be rewritten as
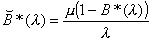 , (3.23)
, (3.23)
which being essentially Equation 3.9 –l is after all an arbitrary positive number – gives that 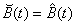 .
.
In order to understand 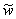 , one needs to define the function U(t) which gives the work
time that remains to be done by the server at time t. If
, one needs to define the function U(t) which gives the work
time that remains to be done by the server at time t. If
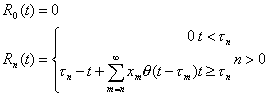 (3.24)
(3.24)
where
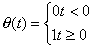 (3.25)
(3.25)
is the heavy side step function, then
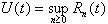 . (3.26)
. (3.26)
U(t) is a nonnegative function that jumps
up xn in height at each
tn.
From these points it descends with a slope of –1 until another jump occurs or
until U(t) = 0. In the latter case it remains flat up to the point where a
new customer arrives. The positive portions of the function represent the
system's busy periods. The complementary idle periods are the segments where U(t)
= 0.
U(t)
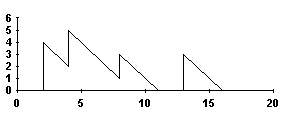 t
t
Figure
3.1
The form of U(t) does not depend on how the customers
are served; however in the FCFS case the remaining work time just before a
customer arrives is that customer's waiting time: 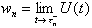 . One may interpret
. One may interpret 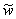 as the equilibrium
remnant work time just before a customer arrives. It is now straightforward to
show that
as the equilibrium
remnant work time just before a customer arrives. It is now straightforward to
show that 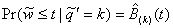 in a LCFS/I system,
and Equation 3.13 then follows. Beneš's inversion of the Pollaczek-Khinchin
Transform Equation, which was developed from a FCFS discipline, is more
closely related to a LCFS/I discipline.
in a LCFS/I system,
and Equation 3.13 then follows. Beneš's inversion of the Pollaczek-Khinchin
Transform Equation, which was developed from a FCFS discipline, is more
closely related to a LCFS/I discipline.
Chapter Four:
G/G/1 (LCFS/I) Systems
Without the exponential distribution analysis of queues
becomes more difficult. Semi-Markov processes can not be used in the same way
as they were used for the G/M/m model: besides the interarrival times the times
between a preceding departure and an arrival become important. The study of
G/G/1 queues centers on ascending ladder points.
4.1. Preliminaries
Set

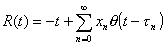 , (4.1)
, (4.1)
where q(t) is again the step function.
R(t) is a function with a –1 slope that jumps up xn at each tn: it is similar to U(t)
except that it descends below zero.
The values just before the jumps will be designated 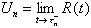 , and the difference in successive peaks will be un = Un+1 – Un for n 0. It can be deduced from
Equation 4.1 that un
= xn – tn+1.
, and the difference in successive peaks will be un = Un+1 – Un for n 0. It can be deduced from
Equation 4.1 that un
= xn – tn+1.
Define a new sequence nk
starting with n1 set such that 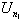 is the first peak to
exceed U0 = 0. Assign nk + 1 so that
is the first peak to
exceed U0 = 0. Assign nk + 1 so that 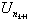 is the first peak
after
is the first peak
after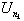 with
with 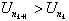 .
. 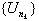 is the set of ascending ladder indices.
is the set of ascending ladder indices.
In a stable queue r <
1 or 1/m - 1/l
< 0. This equation implies that E[un]
< 0, and consequently 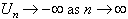 . The result is that there can only be a finite number of
ascending ladder indices. Set K equal
to this number, and designate s = Pr(K 1).
. The result is that there can only be a finite number of
ascending ladder indices. Set K equal
to this number, and designate s = Pr(K 1).
Suppose that R(t) reaches 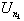 . Since the un's
are independent identically distributed random variables, the probability that
there is a point of R(t) that exceeds
. Since the un's
are independent identically distributed random variables, the probability that
there is a point of R(t) that exceeds 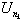 is the same as the
probability that R(t) rises above 0; therefore
is the same as the
probability that R(t) rises above 0; therefore
Pr(K k + 1) = Pr(K 1 ) Pr(K k) = sPr(K k). (4.2)
This leads to
Pr(K = k)
= (1 – s)sk. (4.3)
For K = k, set
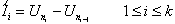 , (4.4)
, (4.4)
and
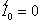 . (4.5)
. (4.5)
The 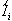 's are also independent identically distributed random
variables. They represent the idle times in the dual queue
where the service and interarrival distributions are swapped. Let F(x)
= Pr(
's are also independent identically distributed random
variables. They represent the idle times in the dual queue
where the service and interarrival distributions are swapped. Let F(x)
= Pr(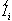 x) and designate its nth
convolution with itself with
x) and designate its nth
convolution with itself with
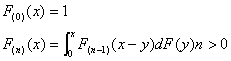 (4.6)
(4.6) 
For the un's
the common distribution function will be
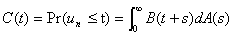 . (4.7)
. (4.7)
It will be important to specify notation for the customers
currently in the queue. If 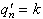 0, then set
0, then set 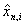 equal to the
remaining service time of the ith
customer still in the queue. The index i
ranges from i = 1 for the customer
that has been there longest to i = k for the most recent one.
equal to the
remaining service time of the ith
customer still in the queue. The index i
ranges from i = 1 for the customer
that has been there longest to i = k for the most recent one.
4.2. A Theorem by D. Fakinos
Theorem: In a G/G/1 (LCFS/I) system,
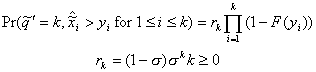 (4.8)
(4.8)
where s and F(t) are defined in the previous section.
Proof. Consider what
is necessary for a stationary distribution:
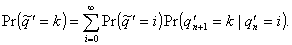
 (4.9)
(4.9)
For k = 0 and n > 0,
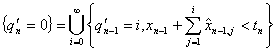 . (4.10)
. (4.10)
In the limit as n this leads to
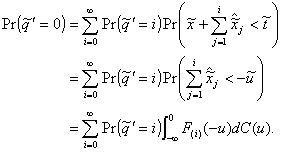 (4.11)
(4.11)
For k > 0 and n > 0,
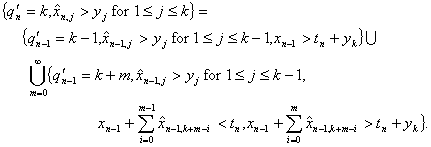 (4.12)
(4.12)
which, in the limit, becomes

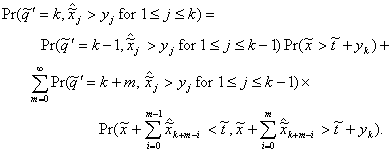 (4.13)
(4.13)
From the preliminary material it may be deduced that
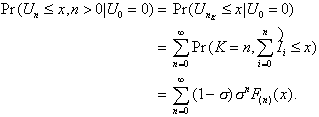 (4.14)
(4.14)
which transforms into
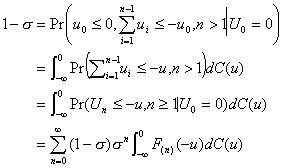 (4.15)
(4.15)
The event 
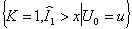 is really the event
that for K = k,
is really the event
that for K = k, 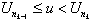 and
and 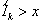 given that U0
= 0. This may be restated as
given that U0
= 0. This may be restated as
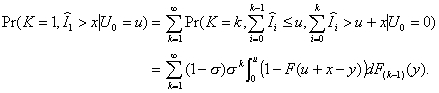 (4.16)
(4.16)
 This leads to
This leads to

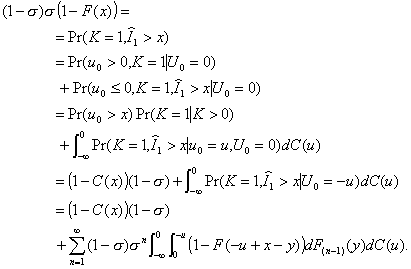 (4.17)
(4.17)
If the theorem is correct, Equation 4.8 must satisfy Equations
4.11 and 4.13. In this light Equation 4.13 becomes
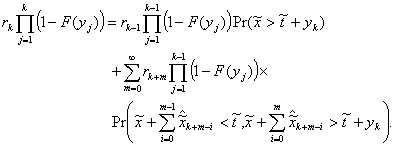 (4.18)
(4.18)
or
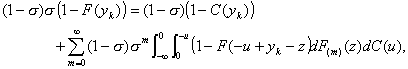 (4.19)
(4.19)
which agrees with Equation 4.17. Equation 4.11 agrees with
Equation 4.15 in the same way. It follows that Equation 4.8 is a stationary
distribution for the system and holds true in the limit.
To show that this solution is unique, note that since r < 1, the state for q' = 0 is non-null persistent. The probability r0 = 1 - s is
independent of the initial state; and when the queue reaches that state the
succeeding condition of the system is independent of preceding conditions. The
queue is ergodic and can only assume the character of the given solution.
4.3 A Result Based on Cooper and Niu's Argument
Usually the semi-Markov process is established solely on the set of arrival instances or
solely on the set of departure instances. Since arrivals and departures affect
the server for a LCFS/I queue, a semi-Markov process can be set up
incorporating both types of events. In this light let
 (4.20)
(4.20)
In this type of system a customer need only "see"
the customers who enter the queue after him. In fact he need only be concerned
with the customers who immediately interrupt his service and consequently
"block" his "view" until they have finished all their
service time. This suggests that changes in state do not depend on the actual
queue length but may be described by the following probabilities:
aa = Pr(arrival | the last event was an arrival)
ad = Pr(arrival | the last event was a departure)
da = Pr(departure | the last event was an arrival) (4.21)
dd = Pr(departure | the last event was a departure)
These are further described by
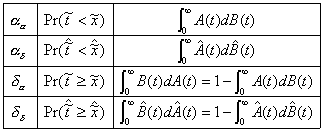
Table
4.1
Here 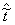 is the residual time
of an interrupted interarrival period:
is the residual time
of an interrupted interarrival period:
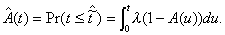 (4.22)
(4.22)
Consider the value of 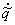 at an arrival:
at an arrival:
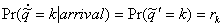 . (4.23)
. (4.23)
Using the same methods of Section 3.3, one gets
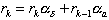 (4.24)
(4.24)
and
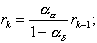 (4.25)
(4.25)
likewise
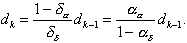 (4.26)
(4.26)
With this,
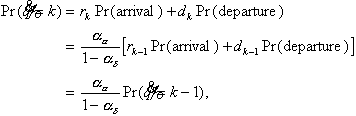 (4.27)
(4.27)
or
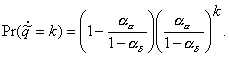 (4.28)
(4.28)
Comparing this with Equation 4.8, one sees that
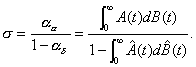 (4.29)
(4.29)
This produces a method for calculating a constant that was
previously defined abstractly.
Chapter
Five: Conclusion
For M/G/1 (LCFS/I) 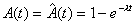 , and Equation 4.29 becomes
, and Equation 4.29 becomes
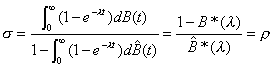 , (5.1)
, (5.1)
which agrees with Equation 3.21. This is only natural since
the calculation of s is a generalization of the calculation
of r.
Again s can be calculated using Equation 4.29:
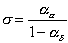 (5.2)
(5.2)
Looking at this more closely, we see that aa, being
the probability that the last change in the system was an arrival, is
equivalently the probability that no departures have occurred in the preceding
interarrival time. ad is then the event
that the system, currently in state Ek,
was last in state Ek+1. Since the system must pass through Ek when going from Ej, j < k,
to Ek+1, ad is actually the
probability that the system does not visit Ek-1 between successive visits to state Ek; thus in accordance with the G/M/1
case,
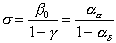 . (5.3)
. (5.3)
The material in the preceding chapter can also be used to
generalize the formula for the waiting time as was developed in Chapter Three:
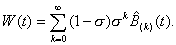
 (5.4)
(5.4)
In form Equation 4.29 parallels the successive-state
probability ratio of other queues with geometrically distributed length. In
calculability it becomes useful in determining quantities like the waiting
time distribution. Understanding the s of LCFS/I queues is being used to give
information about G/G/1 FCFS systems.
.
Bibliography
Bhat, U. Narayan. Elements of Applied
Stochastic Processes, 2nd ed. New York: John Wiley & Sons, 1984.
Cooper, Robert B., and Niu, Shun-Chen. "Beneš's Formula for M/G/1-FIFO
'Explained' by Preemptive-Resume LIFO." Journal of Applied Probability, 23 (1986) 550-554.
Fakinos, D. "The G/G/1 Queueing System with a Particular Queue
Discipline." Journal of the Royal
Statistical Society, B 43 (1981)
190-196.
Kleinrock, Leonard. Queueing Systems, Vol. 1 New York:
Wiley-Interscience, 1975.
VITA
Robert Graham Landrum was born in Bristol, Tennessee, on
August 9, 1966, the son of Mary Fisher Landrum, M.A. and Graham Gordon Landrum,
Ph.D. After attending Tennessee High School, Bristol, Tennessee, he entered
King College, also of the same town, in 1983. He attended Purdue University for
the summer of 1985, and during the summer of 1986, he pursued research at
Lowell Observatory. In May of 1987 he graduated from King College with the
degree of Bachelor of Science. In September, 1987, he entered The Graduate
School of The University of Texas at Austin.
Permanent Address: 2115 Edgemont Avenue
Bristol,
Tennessee
37620-4745
This report
was typed by the author.
Leonard Kleinrock, Queueing
Systems, I (New York: Wiley-Interscience, 1975), pp. 10-18, 396-399.
D. Fakinos, "The G/G/1 Queuing System with a
Particular Queue Discipline," Journal
of the Royal Statistical Society B, 43 (1981) 190.
U. Narayan Bhat, Elements
of Applied Stochastic Processes, 2nd ed.
(New York: John Wiley & Sons, 1984), p. 290.
Robert B. Cooper and Shun-Chen Niu, "Beneš's
Formula for M/G/1-FIFO 'Explained' by Preemptive-Resume LIFO," Journal of Applied Probability, 23
(1986) 550-554.
Cooper and Niu, pp. 552-554.
D. Fakinos, "The G/G/1 Queueing System with a
Particular Queue Discipline," Journal
of the Royal Statistical Society B, 43 (1981), pp. 190-196.
![]() . Limiting distribution functions and their pdf's are written
without a subscript e. g. A(t) and a(t).
. Limiting distribution functions and their pdf's are written
without a subscript e. g. A(t) and a(t).![]() [4]
[4]![]() )
)![]() ) [5]
) [5]![]() and
and ![]() set
set ![]() . Define the utilization factor
. Define the utilization factor![]() where m is the
number of servers. Since it is the ratio of the average arrival rate to the
average service rate for the system, 0 r 1 in order for an equilibrium state to occur;
otherwise the servers will not be able to handle incoming customers fast
enough.
where m is the
number of servers. Since it is the ratio of the average arrival rate to the
average service rate for the system, 0 r 1 in order for an equilibrium state to occur;
otherwise the servers will not be able to handle incoming customers fast
enough. ![]() (1.1)
(1.1)![]()
![]() . (1.2)
. (1.2)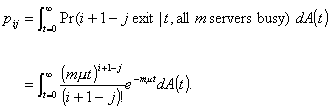
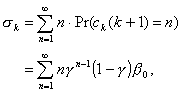
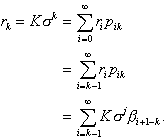
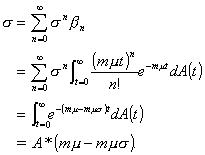
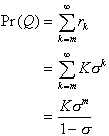
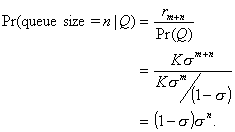
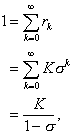

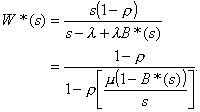
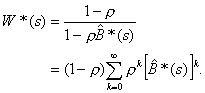
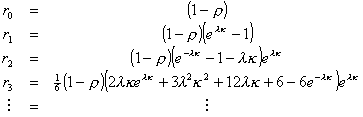
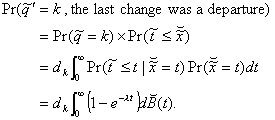
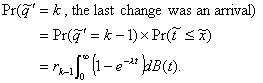
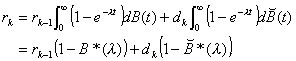
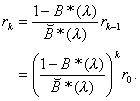
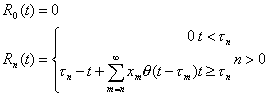
 t
t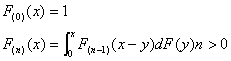
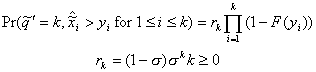
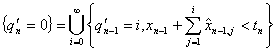 .
.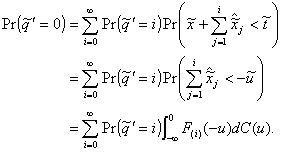
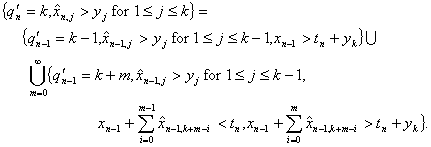
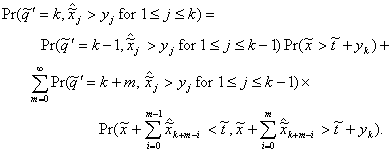
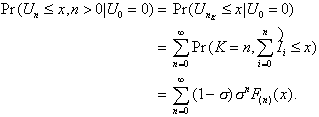
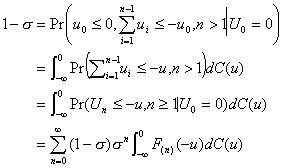
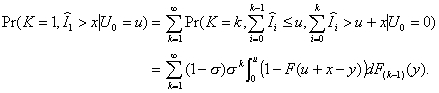
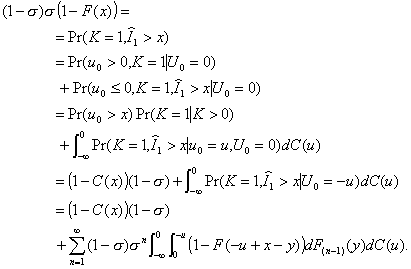
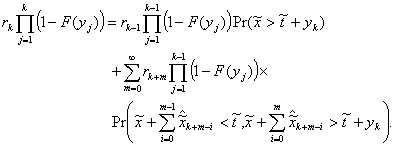
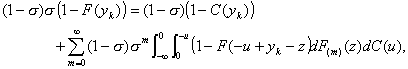
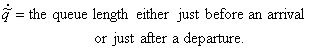
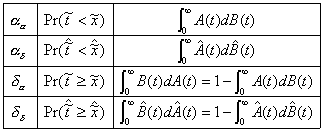
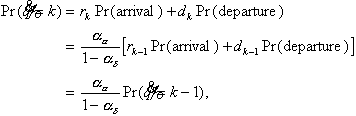
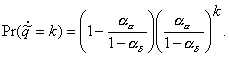
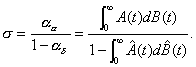
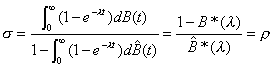 ,
,